Thursday 13 June 2013

Elongation of a bar due to its Own weight

Analysis of a hanging beam:

A BAR HANGING
Let AB is the rod hanging from a ceiling from the end A.
                     Then let, W= Unit weight of the bar,
                                    L= length of bar,
                                   A=Area of cross section,
                                    E= Young's modulus for the bar material

Then elongation of the bar is given by delta ( l )
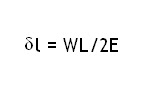Formula of Elongation of a body due to its self weight.


 


                 
The Derivation part is clearly explained in the video!
Posted by at

46 comments:

  1. Unknown27 February 2014 at 20:57

    I believe the equation is wrong. I doesn't include the area.
    It should be deltaL = W*L / (2AE)

    ReplyDelete
    Replies
    1. Unknown22 July 2017 at 22:02

      This comment has been removed by the author.

      Delete
    2. Unknown16 August 2017 at 07:38

      W = w*L
      w = ρ*g
      Elongation = WL/2E = wL^2/2E

      Delete
    3. mayank29 July 2018 at 23:17

      Elongation= WL/2AE= wALL/2AE=wL^2/2E

      Delete
    4. Unknown17 September 2018 at 22:51

      It's right because here unit weight is taken and it is equal to weight/volume= wl/A

      Delete
    5. Unknown17 September 2018 at 22:54

      Unit weight = w/(A*L) so to use it in place of wight A and L are multiplied to have only wight

      Delete
    6. Unknown22 July 2019 at 06:51

      Good and I have got a clear idea

      Delete
  2. Unknown25 April 2015 at 09:18

    in text book elongation= (wl*l)/2e is given

    ReplyDelete
  3. Rajiv18 May 2015 at 07:12

    No, it's actually delta L=WL/(2AE)

    ReplyDelete
  4. anees23 May 2015 at 09:32

    deltaL=WL/2E is correct

    ReplyDelete
  5. Unknown28 June 2015 at 03:13

    The answer is wl/2AE..
    Since we get after integration wl*l/2E,
    we know that Area*l=volume
    so specific weight=m*g/v
    which imples W/v
    on substituting w=W/v
    w*l=W/A
    so elongation =Wl/2AE

    ReplyDelete
  6. Unknown10 December 2015 at 19:35

    There are two formula
    1. If we consider Specific weight of the bar (w in terms of kg/m3), then delta L= wl^2/2E
    2. If we consider weight of the bar (W in terms of kg), then
    delta L= WL/2AE

    ReplyDelete
  7. Unknown8 May 2016 at 16:28

    Thank u... Best answer

    ReplyDelete
  8. Hitesh Daka27 May 2016 at 07:03

    How its derive !?
    Can any budy help ..

    ReplyDelete
  9. Hitesh Daka27 May 2016 at 07:04

    How its derive !?
    Can any budy help ..

    ReplyDelete
  10. Unknown6 October 2016 at 11:19

    This comment has been removed by the author.

    ReplyDelete
  11. Unknown6 October 2016 at 11:20

    This comment has been removed by the author.

    ReplyDelete
  12. Unknown6 October 2016 at 11:20

    Derivation of expression for change in length due to self weight on a uniformly tapering section?

    ReplyDelete
  13. Abhiram Reddy11 October 2016 at 07:25

    If you clearly observe the equation viz.,wl^2/2E where w= unit density, The elongation is clearly proportional to l^2 and independent of Area, So Uniformly tapered bar and Prismatic bar of same length would have same elongation, What ever the size and shape the bar may be. So, no separate derivation is required for uniformly tapered bars. I Hope you are clear, else just ping once again. I'll make a video on it and clearly explain the concept.

    ReplyDelete
  14. Unknown19 October 2016 at 02:55

    there is little bit confusion to take specific weight w and specific density gama. n how both are equal

    ReplyDelete
  15. Unknown2 January 2017 at 09:17

    b chall simply get it that the weight will act at the half of it so just put L/2 at the place of L and you will get the same formula .......... jhanddu baam
    simple bhi bol diya kar kabhi

    ReplyDelete
  16. Emmanuel ike4 June 2017 at 04:14

    Could anyone help me tackle this problem....A copper wire of 2mm diameter ND 35m long is hanging freely from a tower.what will be it's elongation due to its own weight? (take specific weight of cupper : 89.2kN/m³,modulus of elasticity =90*10³N/mm²)

    ReplyDelete
    Replies
    1. Unknown28 June 2017 at 08:12

      Isnt it same problem. You can find W by rho*A*l. Rho is in Kilo newton so multiply by thousand. It wont be in kg but in Newtom

      Delete
  17. Unknown28 June 2017 at 08:09

    Why is Center of mass concept not used for max length at which wire breaks due to its weight.

    ReplyDelete
  18. Unknown14 August 2017 at 02:35

    If u have not knowledge than not posting wrong thing in blog,okk,∆=wL/2AE or YL^2/2E,, because self weight (w)=unit weight*volume=Y*AL, now put these values nd get

    ReplyDelete
  19. Unknown29 August 2017 at 02:10

    If the radius of wire is streched by a load is double , then its modulus of elasticity will be how much ??? Plz Ans Me

    ReplyDelete
  20. Unknown5 December 2018 at 07:39

    Kya bakwas ho Raha h yaha par koi kaam dham nhi h kya

    ReplyDelete
  21. Unknown8 March 2019 at 14:35

    Tensile strength of a material is force over cross sectional area. Doubling the cross sectional area of the bar doubles its weight, but also doubles its strength, so it is correct to say the self supporting length of a bar is independent if its cross sectional area.
    Consider two identical suspended bars, each indepently supporting their own maximum length. Bringing them alongside each other does not change anything.

    ReplyDelete
    Replies
    1. Abhiram Reddy26 December 2019 at 02:27

      Unit weight and length are the only factors influencing the deformation in case of self weight. Unlike in the case of external load where elongation is dependent of area. Hence, you can confidently what ever the area of bar, if of same materials, elongation due to self weight is same.

      Delete
  22. Unknown23 April 2020 at 21:15

    Explained very well, thank you so much

    ReplyDelete
  23. Lol3 November 2020 at 06:08

    Bhot bekar hai ye

    ReplyDelete
  24. Lol3 November 2020 at 06:08

    Koi website pe na aao

    ReplyDelete

Subscribe to: Post Comments (Atom)